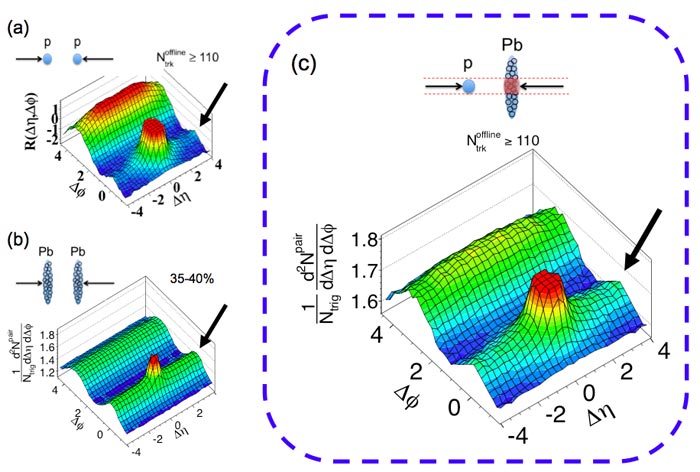
You know that the LHC sometimes collides lead nuclei against lead nuclei instead of proton-proton pairs but a few weeks ago, it tried something something new, the proton-lead (asymmetric) collisions. Physics World tells us about a (not too) surprising result of this hybrid crashing game:
Unexpected 'ridge' seen in CMS collision data againI wrote it's not "too" surprising because it's been seen in gold-gold, proton-proton, and lead-lead collisions, so why it should be missing in the proton-lead collisions? But there's something new about this story I haven't written about yet, and that's the reason for this new blog entry.
It's a new cute and plausible theoretical explanation of the ridge: color glass condensate.
Physics World refers to this fresh paper by a North Carolina-Brookhaven tandem:
Evidence for BFKL and saturation dynamics from di-hadron spectra at the LHCBFKL stands for the Balitsky-Fadin-Kuraev-Lipatov equation which performs a resummation of \(\alpha_S \ln(x)\) terms that appear at each rung of the QCD ladder (here we really talk about Feynman diagrams that look like a ladder with rungs composed of QCD propagators: no kidding). For small \(x\), the right description is in terms of the so-called color glass condensate. You may try to read a funny 2006 paper by Frank Wilczek on the Origin of Mass; full text PDF as a basic background.
The color glass condensate is an interesting new state of matter – composed of quarks – that was proposed in 2000 and that is mathematically analogous to "spin glasses". There are several other cool ways to organize the quarks and their interactions that are intensely studied by some of the creative QCD folks. If I remember well, I learned about another one from a colloquium by Frank Wilczek in Massachusetts – it's called the color-flavor locking.
You know, this blog entry wasn't supposed to be too narrowly focused on the color glass condensate. It's about all similar amusing emergent concepts in QCD and the color-flavor locking is really pretty. ;-) What is it?
Before the color-flavor locking, its fathers have proposed another "behavioral mode" of the quarks in QCD, namely the following condensate (vacuum expectation value):\[
\langle q_i^\alpha C \gamma^5 q_j^\beta\rangle \propto \epsilon_{ij} \epsilon^{\alpha\beta 3}.
\] Here \(i,j\), the Latin indices, represent the flavor (up/down) while the Greek indices, \(\alpha,\beta\), encode the color. You see that the formula above picks the "third color" as a special one so \(SU(3)_c\) is broken to \(SU(2)_c\) while the chiral "flavor" \(SU(2)_L\times SU(2)_R\) group is unbroken.
But in the 1998 paper I have already mentioned, they proposed an even more natural condensate invariant under a "diagonal" \(SU(3)\), namely\[
\eq{
\langle q^\alpha_{Lia} q^\beta_{Ljb} \epsilon^{ab} \rangle &=
-\langle q^{\alpha\dot a}_{Ri} q^{\beta\dot b}_{Rj} \epsilon_{\dot a\dot b} \rangle=\\
&= \kappa_1 \delta_i^\alpha \delta_j^\beta +\kappa_2 \delta_j^\alpha\delta_i^\beta.
}
\] Note that there is no privileged "third color" in this formula. It uses the fact that there are three "pretty light" quark flavors, namely up/down/strange, and three colors. Of course, these two numbers "3" have nothing to do with each other – which is also why the Kronecker delta relating the Greek and Latin indices above is mixing apples and oranges. But because \(3=3\), it is actually possible to choose a random identification and use it to mix apples with oranges – and flavors with colors.
Originally, you had 1st, 2nd, 3rd flavor and 1st, 2nd, 3rd color. These two numbering systems had nothing to do with each other. That's also why you could have rotated the triplets by two independent \(SU(3)\) groups. If Nature ever makes you happy and creates a condensate given by the formula above, the numbering systems for the colors and flavors are identified by the "apple-orange" or "Latin-Greek" Kronecker delta symbols and only an overall \(SU(3)\) group which rotates the colors as well as flavors so that the Kronecker delta symbol is preserved – and these transformations that transform both "versions" of the \(SU(3)\) group in the same way are known as the diagonal group – are preserved symmetries.
Note that the equation above, claiming that the vacuum expectation value has a particular form, is a conjecture. They conjectured that in some situations, it may be true or at least approximately true. But if quarks ever organize themselves so that it is true, it has physical consequences. Alford, Rajagopal, and Wilczek decided that such a condensate would lead to various new "gaps" as well as new Nambu-Goldstone bosons that may be imagined as bound states of two quarks.
Because these "behavioral patterns for quarks" – color glass condensate or color-flavor locking – differ from the usual perturbative QCD that should hold at very short distances, as well as common descriptions of protons, neutrons, and other hadrons, they are considered extreme, perhaps even more extreme than the quark-gluon plasma. But they may have rather non-extreme properties and may be realized in various situations.
From the viewpoint of fundamental high-energy physics, experiments trying to find such exotic forms of nuclear matter are not searching for new physics. Even if those phases exist, they're just manifestations of the good old QCD. However, they are so new and "hard to rigorously calculate" manifestations of QCD that it's pretty interesting, anyway. QCD with colored and flavored quarks has quite some potential for various qualitatively different types of behavior so it's desirable for theorists to propose some initially weird conjectures about what the quarks and gluons could be doing, and for experimenters to check whether the predictions are ever realized.
The ridge seems to agree with some predictions from the color glass condensate and it's pretty interesting. But don't get carried away. Two years ago, I wrote that the ridge could be a sign of the quark-gluon plasma or the dual QCD string. People don't understand these signatures too accurately so the path from the observations to the right interpretations remains somewhat wiggly and shady.
CP violation
BTW, tonight, there will be a new paper on CP violation in D meson decays that will report a 3.5-sigma deviation from the Standard Model in a particular "difference of asymmetries" quantity seen in the 2011 LHCb data.
No comments:
Post a Comment