Evangelista Torricelli: an anniversary

Evangelista Torricelli was born on October 15th, 1608 – we could commemorate his birthday ten days ago – and died of typhoid fever contracted a few days earlier in Florence exactly 365 years ago, on October 25th, 1647.

This early physics worker is mainly remembered for the discovery of the barometer and for his simple law in hydrodynamics.




He was born in the Papal States, was left fatherless as a kid, and was brought up by his uncle. When Galileo was convicted in June 1633, he openly declared himself a member of the "Copernican sect". During the last 3 months of Galileo's life, Torricelli was employed as the master's personal secretary (writer). But what we remember him for is the barometer. An experiment by some random people whom we no longer remember was actually needed to invent the device.



Well, some "engineers" were trying to construct a suction pump, a predecessor of the vacuum pump, for a local Grand Duke of Tuscany. They wanted to raise water by 12 meters. As you may expect, it didn't work quite well: 10 meters was the maximum. Torricelli noticed this experimental lesson and quickly had the idea to replace water by mercury whose density is 14 times higher. He immersed a one-meter-long tube into a vessel with mercury and tried to raise it.



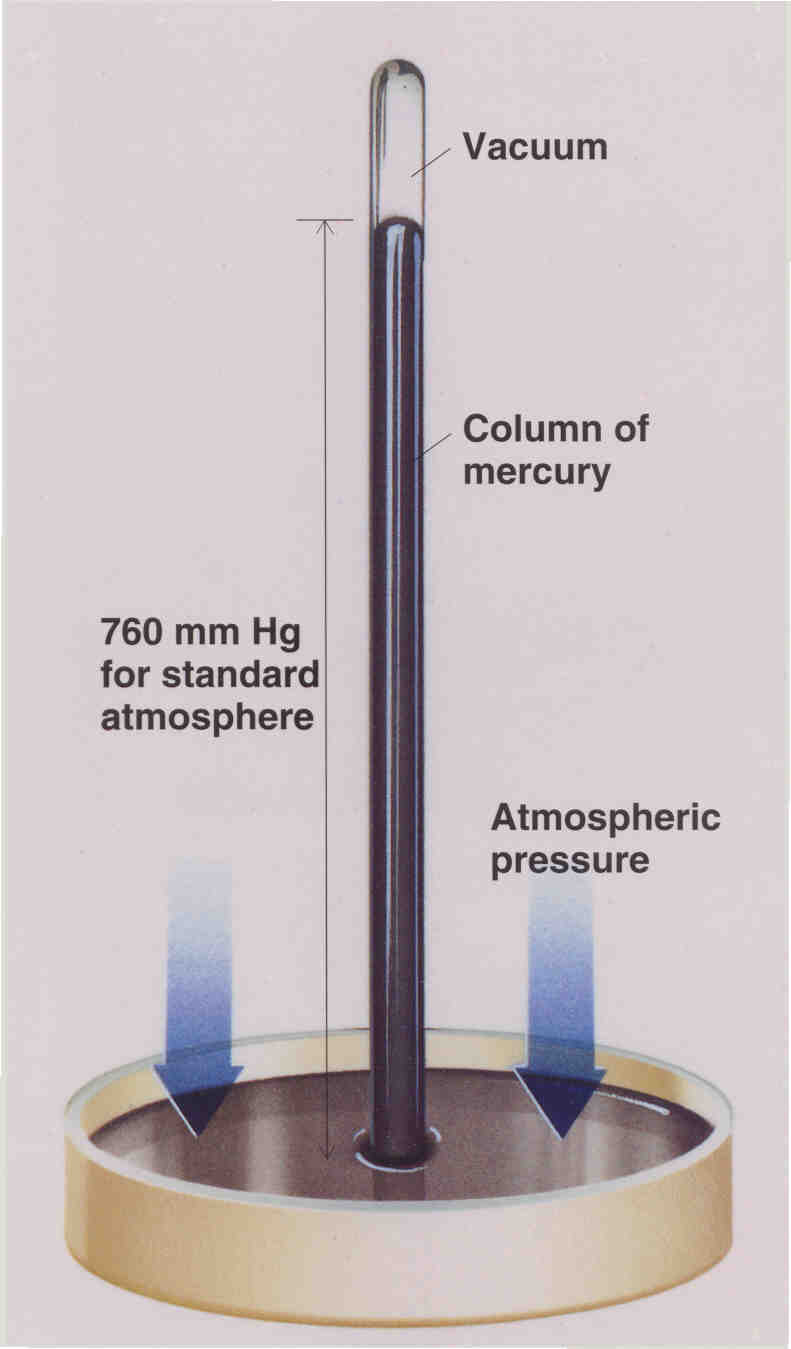
Well, the liquid poison didn't go more than 760 millimeters above the surface level in the vessel. He ultimately realized that the exact height fluctuated, depending on the air pressure. Needless to say, these insights helped Blaise Pascal and others to develop a more detailed understanding of hydrostatics and related questions.



He also discovered Torricelli's law determining the velocity of the liquid sprinkling from a hole at depth \(h\). Of course, the right velocity is\[

v= \sqrt{2 g h},

\] the same velocity that a freely falling object reaches when it starts at the height \(h\). The latter problem is easily solved by comparing the kinetic and potential energy (the latter is changing to the former during the fall),\[

\frac{mv^2}{2} = mgh,

\] but it also holds for the water molecules because the kinetic energy of the water in the vessel is negligible (as it scales with the second power of the speed which is very low) and there are two changes affecting the vessel: molecules are disappearing from the surface; and some other molecules are sprinkling from the hole at depth \(h\).

So the lost potential energy of the "disappearing molecules at the surface" which were moved to the hole (it doesn't matter which molecules are which, we're only computing the energy) has to be converted to the only other term in energy we see, the kinetic energy of the sprinkling water, so we inevitably get the same formula for the speed.

Torricelli's law got generalized to Bernoulli's law some years later.\[

{v^2 \over 2}+gz+{p\over\rho}=\text{constant}.

\] It's still an energy conservation law in one form and relatively to the equation equivalent to Torricelli's law, it also contains the extra pressure term \(p/\rho\) which acknowledges that the pressure may also change due to other reasons and the internal energy of the liquid also depends on the pressure (pressure is a sort of energy per unit volume and all the terms in the equations are forms of "energy per unit mass" which is why the pressure has to be divided by the density \(\rho\)).

Torricelli also discovered his trumpet, also known as Gabriel's horn, whose volume is finite but the surface is divergent. It was considered to be an incredible paradox by various people who sucked in maths. Torricelli didn't suck in maths; instead, he was able to suck liquids but only up to the height \(p_{\rm atm.}/(\rho g)\), as we mentioned. He knew how to find out which series (and, indirectly, integrals) converged and which didn't. This also led him to realize that there exist telescoping sums – something that helped me to earn $300 a few weeks ago – where most of the terms cancel. If a sum may be rewritten as\[

(a_0-a_1)+(a_1-a_2)+(a_2-a_3)+\dots + (a_{n-1}-a_n),

\] the result is clearly \(a_0-a_n\). Some interesting sums may actually be rewritten – either exactly or approximately – in this form which allows us to quickly calculate or at least estimate the result (or prove that it converges when it does).

Why don't we remember the engineers who tried to construct the 12-meter water suction pump? Is it unfair? I don't think so. They didn't think about their "failure" too much. A true physicist must be able to notice patterns and convert "unpleasant surprises" to "great new insights" whenever it's possible. Torricelli knew how to do that which is why he was more important than the engineers who made the random discovery.