The holographic principle

The newest episode of The Big Bang Theory that was aired last night was called "The Holographic Excitation" (S06E05).

It's pretty cool that a TV sitcom manages not only to show a hologram but Leonard Hofstadter was even allowed to present a rather accurate definition of the holographic principle in quantum gravity i.e. string theory (you won't find it in any popular science TV program that claims to explain modern physics!). And as a result, he was able to have an intercourse with Penny right after she wore some glasses and was shown a moving holographic pencil and a moving holographic globe. (Later, he repeated the same achievement using Maglev.)

(And I even think that Prof Nina Byers whom I know rather well walks behind the main actors around 9:15. This theory seems to make sense because she's at UCLA, much like the TBBT science adviser David Saltzberg.)



The holographic principle of quantum gravity is an incredible example of the ability of the quantum gravity and string theory research to teach us things we really didn't and perhaps couldn't anticipate, force us to modify or abandon some prejudices, and adopt ideas about the unification of ideas and concepts that philosophers couldn't have invented after thousands of years of disciplined reasoning but physicists may be forced to realize them if they carefully follow the mathematical arguments sprinkling from a theory that they randomly discovered in a cave.

But let's return half a century into the past. Holography started in "everyday life physics" in the late 1940s.




So let us begin with this exercise in wave optics that has nothing to do with quantum gravity or string theory so far – but you will see that it exhibits a similar mechanism that is apparently "recycled" by the laws of quantum gravity.

Dennis Gabor's 3D images

Hungarian-British physicist Dennis Gabor was playing with X-ray microscopy and invented a new technology that is rather cute. One may create two-dimensional patterns on a piece of film which, when illuminated by a laser, create the illusion of a three-dimensional object floating in the space around it. I saw my first hologram sometime in 1985 – it was a Soviet one, the mascot of the 1980 Olympics in Moscow – in the National Technological Museum in Prague where we went to a school excursion. I couldn't believe my eyes. :-)

The basic setup involves a monochromatic laser beam, some interference, and a photographic plate. First, we must create the hologram – a film with strip-like patterns that don't resemble the bear at all but which allow the bear to jump out once you use another laser. Fine. Let's create a hologram.



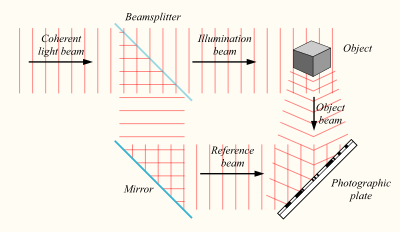
You see that a monochromatic (one sharp frequency) laser beam is coming from the upper left corner. Each photon's wave function gets divided into two portions by a beam splitter – note that the wave function has a probabilistic interpretation for one particle but if many photons are in the same state, it may be interpreted as a classical field.

Two parts of the wave are moving from the beamsplitter. One gets reflected from a simple mirror. More interestingly, the other one gets reflected from the object we want to see on the hologram. They interfere – these waves are recombined – in the right lower corner and they create a system of interference strips on the photographic plate.

We have created a hologram and now we may sell it. What will the buyers do with it?



This interference pattern may be shined upon by a "reconstruction beam" of the same frequency and what we see is a virtual image behind the plate. You may actually move your head and eyes and the position of all points on the image are moving just like if the virtual image were a real object. So it's not just a stereographic image offering two different pictures for the two eyes: the hologram is ready to provide the right electromagnetic field regardless of the direction from which you observe it! If you want to see the right face of the object, you move your head to the right side, and so on.

Why does it work? It's very useful to think about the hologram for a simple object, e.g. a point at a given distance. The total wave function on the photographic plate parameterized by coordinates \(x,y\) is given by \(U_O + U_R\) where \(U_O\) is the complicated wave reflected from the object and \(U_R\) is the simple reference beam reflected from the plain mirror.

You may imagine that for an object being a point, \(U_R=1\) and \(U_O(x,y)=\exp(iks(x,y))\) where \(s\) is the distance between the point (the real object we want to holographically photograph) and the given point \((x,y)\) on the photographic plate. The wave number is of course the inverse wavelength, \(k=2\pi/\lambda\). The sum \(U_R+U_O\) gives you some simple concentric circles (with decreasing distances between neighbors) around the point on the plate that is closest to the photographed point. Fine. The total intensity – how much the point on the film changes the color – is given by \[

T \sim \abs{U_O}^2 + \abs{U_R}^2 + U_R^* U_O + U_O^* U_R.

\] I omitted an unimportant overall normalization and used the symbol \(T\) for this quantity because the darkness of the point of the film will be interpreted as the transmittance, the ability of the place of the hologram to transmit the other, reconstruction beam when we actually want to reconstruct the image.

For a simple explanation why you will see the reconstructed virtual image, assume that the reference beam \(U_R\) is much stronger than the object-induced wave \(U_O\) i.e. \(U_R\gg U_O\). So the total wave function may be written as \[

U = 1 + \varepsilon \exp(iks)

\] where \(\varepsilon\) is small, \(\varepsilon\ll 1\). You see that the squared absolute value is\[

T \sim |U|^2 = 1 + \varepsilon \exp(iks) + \varepsilon \exp(-iks) + {\mathcal O}(\varepsilon^2).

\] Imagine that this transmittance is just multiplying another simple reference beam \(U_R\to T \cdot U_R\) and produces some electromagnetic field in the vicinity of the hologram. For the sake of simplicity, assume \(U_R=1\) again. It's only \(U_O\) that carries the "complicated information about the photographed object" but we still need some nonzero \(U_R\).

You may see that \(T\) is almost the same thing as \(U\) except that it has an extra, complex conjugate term. So the electromagnetic field in front of the hologram (on the side with the air) will be the same field as the electromagnetic field we used to have when there was a real object in front of the hologram plus some complex conjugate term. One of these terms creates a nice virtual image behind the plate because it has a similar mathematical structure and when the fields have the same values, we see the same thing.

The other term induces the feeling of another copy of the object – a real image. It's because all the waves should also be multiplied by the universal time-dependent factor \(\exp(-i\omega t)\) (before you interpret the real and imaginary value of the overall sum as the electric and magnetic fields, respectively, kind of) and the complex conjugation is equivalent to \(t\to -t\) which means that the wave is kind of moving backwards in time which is effectively equivalent to moving from the other side of the mirror.

So when you look at the hologram, you actually see one virtual image behind the plate and one real image in front of the plate (which may overlap with your head). I don't want to figure out which term is which because odds would be close to 50% that my answer would be wrong. To be sure about the answer to this not-so-critical question, I would have to decompose the electromagnetic wave to the electric and magnetic components, consider \(x\) and \(y\) polarizations, be careful about the spatial dependence and all the signs, etc. But things clearly work up to this "which is which" question that I am not too interested in.

In this brute calculation, I have neglected the \({\mathcal O}(\varepsilon^2)\) terms which indicates that the hologram will be badly perturbed if \(\varepsilon\sim {\mathcal O}(1)\) but a more accurate analysis shows that the result won't be too bad even if you include these second-order terms. At any rate, I have created a virtual image of a point! By the superposition principle, you are allowed to envision any object to be composed of many points (perhaps as an "integral of them") and add the terms \(\exp(iks_P)\) from each point \(P\) and you get the idea how it work for a general object.

There exist generalizations – colorful holograms, perhaps moving holograms and holographic TV, and so on, but I don't want to go into these topics on the boundary of physics and engineering. Everyone knows that holograms are cool. What's important for us is that they store much more than some two-dimensional projections of a 3D object as seen from one direction or two directions; they store the information about the 3D object as seen from any direction (in an interval). They're the whole thing.

Instead of discussing advanced topics of holography in wave optics, we want to switch to the real topic, the holographic principle in quantum gravity.

The holographic principle

In the research of quantum gravity, the notion of holography was introduced by somewhat speculative but highly playful papers by Gerard 't Hooft in 1993 and Lenny Susskind in 1994. Charles Thorn is mentioned as having suspected similar ideas for years.

It may sound unusual ;-) but Lenny Susskind's paper was the technically more detailed one, getting well beyond the hot philosophical buzzwords. Susskind also suppressed some unjustified and unjustifiable "digital" comments by 't Hooft who had written that the information had to be encoded in binary digits (bits). Of course, there's no reason whatsoever why it couldn't be trinary digits, other digits, or – much more likely – (for humans and computers) some much less readable but more natural codes.

What's the basic logic behind holography in quantum gravity?

In classical general relativity, a black hole is the final stage of the collapse of a star or another massive object. Because the entropy never decreases, as the second law of thermodynamics demands, the "final stage" must also be the stage with the maximum entropy. So the black hole has the highest entropy among all bound or localized objects of the same mass (and the same values of charges and the angular momentum). I emphasize the adjectives "bound or localized" because delocalized arrangements of particles with a given total energy – e.g. the Hawking radiation resulting from a black hole that has already evaporated – may carry a higher entropy (that's inevitably the case because the process of Hawking radiation must be increasing the total entropy, too).

But we've known from the insights by Jacob Bekenstein and Stephen Hawking in the 1970s that the black hole entropy is\[

S_{BH} = \frac{A}{4G}

\] in the relativistic \(c=\hbar=1\) units. It's one-quarter of the area of the event horizon \(A\) in the units of the Planck area. In normal units, you must replace\[

G \to l_{\rm Planck}^2 \equiv \frac{G\hbar}{c^3}.

\] So the maximum entropy of a bound localized object of a given mass is actually given by the area of the black hole of the same mass. Because you can't really squeeze the matter into higher densities than the black hole, the black hole is also the "smallest object" that may contain the given mass.

To summarize, we see that the black hole is the "highest entropy" object as well as the "geometrically smallest" object among localized or bound objects of the given mass. It follows that it also maximizes the "entropy density" (entropy per unit volume) among the localized arrangement of matter of the same total mass. But the entropy carried by a black hole is only proportional to the surface area in the Planck units, \({\mathcal O}(R^2)\), so the entropy density per unit volume – the latter scales as \({\mathcal O}(R^3)\) – is therefore going to zero for large black holes i.e. for large masses or large regions.

The maximum density of entropy or information you may achieve with a given mass is actually going to zero if the mass is sent to infinity. If you try to squeeze too many memory chips into your warehouse, they will start to be heavy at some point and will gravitationally collapse and create a black hole which will have a certain radius – either smaller than or larger than your warehouse. At any rate, this black hole will only be able to carry \(1/4\) of a nat (a bit is \(\ln(2)\) nats) of information per unit surface area (by the surface, I mean the event horizon).

We see that the maximum information is carried by a constant density per unit area rather than the unit volume. You should appreciate how shocking it is. In some sense, it was completely unexpected by virtually all experts in the field. Quantum field theories predict some new phenomena at a characteristic distance scale. For example, Quantum Chromodynamics (QCD) says that quarks like to bind themselves into bound states where their distance is comparable to the QCD length scale, about one fermi or \(10^{-15}\) meters. So by the dimensional analysis, the only sensible "density of information" we may get in QCD is "approximately one bit per cubic fermi" or per "volume of the proton".

People would expect a similar thing in any QFT – which was mostly right – but they thought it would also hold in quantum gravity. So quantum gravity may achieve "one bit per Planck volume". But that was wrong. You see that the previous paragraph assumed a bit more than the dimensional analysis: it also implicitly and uncritically postulated that the information is proportional to the volume. This assumption followed from locality. But this assumption breaks down in quantum gravity where the information only scales as the surface area.

Because the "proportionality to the volume" is linked to "locality" – each unit volume is independent from others – the violation of the "proportionality of the information to the volume" that the holographic principle forces upon us also means that locality is violated, at least to some extent. And indeed, this violation of the locality is a fact responsible for the resolution of other puzzling questions in quantum gravity, too. In particular, some tiny and hard to observe but nevertheless real non-locality occurs during the evaporation of the black hole which is why the information may get from the black hole interior to infinity, after all – even though classical general relativity strictly prohibits such an acausal export of the information (locally, it's equivalent to the superluminal transport of information which was already banned in special relativity). In quantum gravity, this "ban" is softened because the information may temporarily violate the rule in analogy with the quantum tunneling. In fact, the black hole evaporation is a version of quantum tunneling.

Whether the holographic principle was real and what it exactly it meant and what it didn't mean remained a somewhat open question for 3 more years or so. However, at the end of 1997, Juan Maldacena presented his AdS/CFT correspondence which is a set of totally controllable mathematical frameworks in which holography holds. The information about a region – namely the whole anti de Sitter space – is stored at the boundary of the region – which is the asymptotic region at infinity which nevertheless looks like a "finite surface of a cylindrical Penrose diagram" if you use the language of Penrose causal diagrams.

The holographic principle surely captures the right "spirit" of quantum gravity but it is a bit vague. The AdS/CFT correspondence is a totally well-defined "refinement" of the holographic principle but it is arguably too special. Nevertheless, one must be careful about deriving potentially invalid corollaries of the holographic principle in other contexts.

For example, if you replace the anti de Sitter space by a finite-volume region of ordinary space, it seems clear to me that the holographic principle will only be true in some rather modest sense: it will be true that the entropy bounds hold. You can't squeeze too much entropy into a given region. However, if you will try to find the "theory on the boundary" that is equivalent to the evolution inside the region, you will find out that such a theory on the boundary "exists" – but the existence of such a theory is just an awkward translation of the ordinary evolution to some artificial degrees of freedom that you placed on the boundary.

What is special about the AdS/CFT correspondence is that the theory on the boundary is a theory of a completely normal type – namely a perfectly local, conformal quantum field theory. In fact, the boundary theory is more local than the gravitational theory in the bulk – because we just said that the gravitating theory in the bulk must be somewhat non-local. I am confident this fact depends on the infinite warp factor of the AdS space at infinity and won't hold for finite regions. In other words, I think that the "holographic theory living on a boundary" of a generic finite region won't be local in any sense – the boundary still has a preferred length scale, the Planck length, and other things so it is surely not conformal etc. And because it won't be local, it won't be simple or useful, either.

So one shouldn't generalize the holographic principle as seen in the AdS/CFT correspondence too far and too naively.

Lessons

In the 1970s, people got used to Ken Wilson's "Renormalization Group" inspired thinking about all effective field theories. Each theory predicted some phenomena at a characteristic length scale. The third power of the length scale gave us a characteristic volume. And one could expect roughly one nat (or bit) per one characteristic volume. It was nice, it made sense, it has lots of applications.

But Nature sometimes has surprises in store and quantum gravity had one, too. You may still use almost the same logic – one nat per unit region – but the region must actually be measured by its surface area, not its volume. So quantum gravity tells us that one of the spatial dimensions may be thought of as an "artificial" or "emergent" one and other mechanisms supporting this general paradigm have appeared as well.

A brutally arrogant yet extremely limited physicist who really sucks – think of Lee Smolin, for example – may think that he has all the right ideas how the final theory should look like from the beginning. Except that none of them works (except as tools to impress some stupid laymen). But other physicists who are much smarter but much more modest may see that all Smolin's prejudices are just wrong and Nature's inner organization is much more clever, creative, surprising, and forcing us to learn new concepts and new way of thinking more often than Smolin and many others would expect. One must still be ingenious or semi-ingenious to discover some important wisdom about Nature – e.g. holography and the AdS/CFT correspondence – but Nature just doesn't appreciate men who try to paint themselves as wiser than herself. Science is the process of convergence towards Her great wisdom; it is not a pissing contest in which idiots such as Lee Smolin try to pretend that they're smarter than Nature.

The story of the holographic principle also shows us that Nature recycles many ideas. The fields defined on the boundary CFT in the AdS/CFT correspondence literally emulate the waves \(U\) and \(T\) that I mentioned in the discussion of the "ordinary" holography by Dennis Gabor.

And the story of the holographic principle is another anecdotal piece of evidence in favor of the assertion that string/M-theory contains all the good ideas in physics. 't Hooft and Susskind, building on the work by Bekenstein, Hawking, and others, had some "feelings" about the right theory of quantum gravity and there had to be something right about them. And indeed, string theory showed us that they were mostly right. Because string theory is a much more mathematically well-defined a structure than "quantum gravity without adjectives", it also allowed us to convert the philosophical speculations into sharp and rigorous mathematical structures and equations and decide which of the philosophical speculations may be proven as meaningful ones and which can't.

The holographic principle is also another step in the evolution of physics that makes our theories "increasingly more quantum mechanical". While the spacetime remains continuous, we see that the information in a region may be bounded in unexpected ways and a whole dimension of space may be emergent. Needless to say, the equivalence between theories that disagree about the number of spacetime dimensions is only possible if you take the effects of quantum mechanics into account.

Alan Guth on himself, science, cosmology

Aside from Edward Witten, another well-known winner of the Newton Medal (in 2009) was Alan Guth, the first father of cosmic inflation. Two month ago, the Institute for Physics posted the post-Newton-Medal interview with him, too.



He had no science background in his family. At least he doesn't remember any background. But his family was happy when it learned that Alan was into science. Well, they were happy for a while, before they realize that science wasn't quite the same thing as engineering, but it was fortunately too late for them intervene. ;-)

He grew up in a small town, Highland Park, New Jersey which only has 15,000 inhabitants or so today. Well, it may be a small town but your humble correspondent knows it very well from his Rutgers years (1997-2001). In fact, I officially had a physician over there although I have never visited him so at least, I was sometimes going to do shopping in a grocery store over there. You may guess what Guth's father was: Yes, he had a grocery store in Highland Park. It burned at some point. ;-)




Many or most people in the Academia and especially theoretical physics come from scholarly families – the tradition usually goes back several generations, in fact. It has advantages and it has disadvantages. This "inherited occupation" adds some amount of sterility to the environment. On the other hand, the "scholars who inherited the job" are trained to be productive scholars so I am pretty sure that in average, they write many more papers than the "first explorers of the scientific occupation in a family". The latter may often be more audacrious and creative, however.

Guth was affected by a fabulous high school teacher. He didn't know too much physics, Alan Guth later realized, but he was still lucky to have a dynamic guy of this type. He described some success of him as a theoretical physics when he was a high school pupil – something based on a pure thought but it still works well. ;-) Alan Guth married his high school sweetheart. Two kids, the son is a mathematician who proved e.g. the Son-of-Guth Theorem (naming convention due to Susskind, if I caught it well).

MIT was where he went to college. MIT was unusual socially because it didn't separate people who are "in" and "out". He liked it. He was surprised he had superior competitors – unthinkable at the high school. People specialized a bit. He became sure he wanted to be a theoretical physicist. Grad school. Postdoc jobs. One of them made him interested in cosmology. Magnetic monopoles in the early Universe became his important obsession.

Alan Guth explains what cosmology is – science of the Universe as a whole, especially focusing on its childhood. The Big Bang Theory was great but it needed things to be fine-tuned and failed to explain the uniformity, too. He discovered cosmic inflation while solving another problem, namely why Sheldon Cooper of The Big Bang Theory has't found magnetic monopoles during their polar expedition. Guth explains why inflation gives the bang to the Big Bang. A gram of matter is enough to create our large visible Universe. A gram is not much but it's still much more than the Planck mass so it's not a theory of everything.

It looked dramatic so he was afraid it was wrong but after some talks, especially those with big shots in the audience, it became clear it wasn't wrong. Today, cosmology is in the golden age, indeed. Things are accurate. He describes the composition of the Universe and the absolute nothingness at the beginning. God is pointless because because He is just a redundant connecting link – with this addition, you must just explain why He is there instead of the Universe. ;-)

Hat tip: Joseph S.

Edward Witten on science, strings, himself

Two months ago, the Institute of Physics revealed this YouTube video:



Edward Witten, whom they still call "a 2010 Newton Medal Winner" rather than the "An Inaugural Milner Prize Winner" because they think that £1,000 with a stamp "IOP" on it (plus the name of Isaac Newton, without his permission) is more than $3,000,000 ;-), is talking for 25 minutes about his CV, previous scholarly interests, as well as hot topics in string theory.




Edward Witten is known for having studied some social sciences – journalism, history, linguistics – and being a tool of the Democratic Party candidates (such as George McGovern 1972 who just died) but he has been interested in physical sciences from his childhood. He was interested in astronomy but he was afraid that the job required him to be an astronaut. It is cute to mix astronomers and astronauts. My dad doesn't distinguish astronomers from astrologers.

Of course, his father – a theoretical physicist – was probably affecting Edward Witten, too.

He has been interested in the peace in the Middle East. In fact, some of his $3 million Milner money is going to J Street, a left-wing NGO trying to create peace between the Israeli Arabs and Jews in some of the most naive ways. Of course, just like anyone who takes string theory seriously, he shows an old picture of himself on a camel.

He talks about his wife, kids, and interests. His parents didn't believe in pushing kids too far too quickly. He got a standard theoretical physics education rather soon. Only when he was a postdoc, his maths was getting deeper. Supersymmetry became essential when he was a student. It has played a key role in his research from the beginning.

Some extra remarks are dedicated to Einstein's general relativity, extra dimensions, and unification of all forces. He talks about his negative-energy instability of higher dimensions without SUSY. He paints himself as a relative latecomer to string theory. Of course, it depends whom you compare him with. Witten compares the beauty of the sound of different musical instruments depending on the admixtures of the higher Fourier modes.

In the early 1980s, he realized that the available consistent string vacua failed to violate the left-right symmetry (P and CP). At some moment in 1984, the first superstring revolution explodes and it was the first string miracle that occurred when Witten was watching. That's why it was a signal from the Heaven for him. String theory got much more realistic.

The 1990s are the decade of dualities and M-theory. Who needed the other four string theories, and so on. From that time, he's been intrigued by the application of string/M-theoretical methods to understand issues in "ordinary" established particle physics theories (why positive energy, why confinement, ...). This light that string theory manages to shine upon the established theories is Witten's main reason to be convinced that string theory is on the right track. The elegance with which string theory sheds the light is another reason. Witten still calls our understanding of string theory "the rough draft" but this rough draft has already led to amazing insights and Witten doesn't believe that such a chain of astonishing discoveries has happened by coincidence.

The last reason why string theory seems right to him is that it teaches us new and deeper things about the geometry – including things that surprised mathematicians and inspired those at the frontier. He hadn't expected such a thing when he was young but these insights did materialize. Our confusion has actually helped to develop the new concepts.

A special discussion is dedicated to the big mystery what is the core principle underlying string theory much like the equivalence principle or spatial curvature underlying Einstein's general relativity. What string theory really means? It fascinates him most. But for decades, the theory has been smarter than us and forced us to move in previously unanticipated direction with twists – and that's probably still true today.

Witten isn't actively trying to solve the biggest questions. He says a thing often told by Andy Strominger as well – an important skill in the research is to choose a question small enough so that you have a chance to answer it but big enough so that it is worth answering. The Khovanov issues are mentioned as an example. Witten couldn't understand what the stuff was about – but he did understand it was physics-related (I am not that far). Witten makes it clear he realizes that most string theorists aren't interested in those things but he's independent enough not to care. Of course, there's no guarantee this stuff will be important. He knows that but he suspects it will be important. ;-)

At the end, he compares the string theory research with the discovery of new continents and with finding a treasure underground that we don't fully understand but we see that pieces fit together.

New element

Some fun via Fred S. – a new densest element was just found.

How empty is the black hole interior?

This article is a continuation of the discussion of black hole firewalls.



I've exchanged a dozen of e-mails with Joe Polchinski, the most well-known physicist in the original team that proposed the firewalls. We haven't converged and Joe ultimately decided he didn't have time to continue and recommended me to write a paper instead (which he wouldn't read, I guess). However, he started to listen to what my resolution actually is and I could see his actual objection to it which seems flawed to me, as I discuss below.




Recall that \(\heartsuit\) represents the (near) maximum entanglement and the firewall folks demonstrate that because \(R\heartsuit R'\), the following things hold:\[

A\heartsuit B, \quad R_B \heartsuit B.

\] The degrees of freedom \({\mathcal O}(r_s)\) outside the black hole at \(t=0\) when the black hole gets old are maximally entangled with some part \(R_B\) of the early Hawking radiation (because \(R\heartsuit R'\)) as well as with the degrees of freedom inside the black hole \(A\) which are "mirror symmetrically" located in the other Rindler wedge from (infalling) Alice's viewpoint.

But because a system can't be maximally entangled with two other systems, there is a paradox and one of the assumptions has to be invalid. AMPS continue by saying that what has to fail is the "emptiness of the black hole" assumption. They make another step and say that all field modes inside the old black hole are hugely excited so an infalling observer gets burned once she crosses the event horizon.

My answer is that the resolution is that \(A\) and \(R_B\) aren't really "two other systems"; \(A\) is a heavily transformed subset of degrees of freedom in \(R_B\) so \(B\) is only near-maximally entangled with one system, not two, and everything is fine. I believe that this has been the very point of the black hole complementarity from the beginning.



Yup, I took this picture in Santa Barbara, not far from the KITP.

Now, Joe's objection is the following:

Even Alice must have a state, a pure state or a mixed state, ready to make predictions. Up to \(t=0\), she describes the early Hawking radiation in the same way as Bob (who stays outside). For example, this wave function may imply that \(N_b=5\) for an occupation number measured outside the black hole; the state may be an \(N_b=5\) eigenstate.

It also means that the state is an eigenstate of a (complicated) observable at a later time which evolved from \(N_b\). On the other hand, this observable doesn't commute with \(N_a\), the occupation number for a field mode moderately inside the black hole, in the \(A\) region. The state can't be an \(N_b\) eigenstate and an \(N_a\) eigenstate at the same moment because they're generically non-commuting operators, and consequently, it can't be true that \(N_a=0\) which is needed for the emptiness of the old black hole interior from the viewpoint of an infalling observer.

This is Joe's paradox readjusted to "my" resolution. Is this paradox real?

I don't think so. What is true and what is not about Joe's statements above?

First, let us ask: Will her "later" state be an eigenstate of \(N_a\) or \(N_b\)? Here, the answer is clear. We assumed the state to be an \(N_b=5\) eigenstate so by the dynamical equations, the state will remain an eigenstate of an observable that evolved from \(N_b\) via Heisenberg's equations. For this quantity (probably involving an undoable measurement in practice), the measured value is sharply determined.

To predict the value of another quantity such as \(N_a\), we need to decompose the state into \(N_a\) eigenstates and the squared absolute values of the probability amplitudes determine the probabilities of different results. Joe is right that in principle, because the operators \(N_a\), \(N_b\), and their commutator are "generic", there will inevitably be a nonzero probability for \(N_a\neq 0\).

However, Joe isn't right when he suggests that this means a problem. Indeed, the probability of \(N_a\neq 0\) will be nonzero. Nevertheless, this probability may still be tiny. In other words, the probability that a particular mode will be seen as \(N_a=0\) may still approach 100 percent so in the classical or semiclassical approximation, quantum gravity will continue to respect the equivalence principle which implies that an observer falling into an old black hole sees no radiation (not even the Unruh one which he would see if he were not freely falling).

And I think that this is what happens. The probability of \(N_a\neq 0\) is tiny but nonzero. We may try to be somewhat more quantitative.

Choose a basis of the \(\exp(S)\)-dimensional space of the black hole microstates so that the basis vectors are \(N_a\) eigenstates. Now, my point is that the number of \(N_a=0\) basis vectors can be and almost certainly is greater (and probably much greater) than the number of \(N_a=1\) or higher eigenvalue eigenstates. We know how it would work if \(N_a\) were counting the occupation number from a non-freely-falling, "static" observer's viewpoint.

In that case, the probability of having a greater number of particles (by one) would be suppressed by a factor similar to the Boltzmann factor \(\exp(-\beta E_n)\) where \(E_n\) is the energy of the mode and \(\beta\) is the inverse black hole temperature, comparable to the Schwarzschild radius. In that case, we could prove that the probability of having a higher number of particles (by one) in some spherical harmonic \(Y_{LM}\) would be suppressed by something like \(e^L\); I am a bit sketchy here. This is just a description of the Unruh radiation that a "static" observer would experience right outside the black hole.

Things are harder for the freely infalling observer. Classically, she shouldn't see any radiation – because of the equivalence principle – so the higher values of \(N_a\) should be even more suppressed. The suppression should become "total" for macroscopic black holes.

At the same time, however, the working of the low-energy effective field theory means that in the relevant Hilbert space, the creation operator increasing \(N_a\) must relate states pretty much in a one-to-one fashion. So how it could be true that the number of \(N_a=1\) eigenstates in the basis is (much) lower than the number of the \(N_a=0\) eigenstates?

Before you conclude that my scenario is shown mathematically impossible, don't forget about one thing. If you create a quantum in a quantum field (in the black hole interior) and increase \(N_a\), you also change the total mass/energy of the black hole from \(M\) to \(M+E_a\). So the \(N_a=0\) states of a lighter black hole are in one-to-one correspondence with the \(N_a=1\) states of a heavier black hole.

In other words (or using an annihilation operator), the \(N_a=1\) states of the black hole of a given mass are in one-to-one correspondence with the \(N_a=0\) states of a lighter black hole whose mass is \(M-E_a\). But a smaller black hole has a smaller entropy, and therefore a smaller total number of all microstates. The ratio of the number of states is approximately equal to\[

\frac{ \exp(S_{\rm larger})} {\exp(S_{\rm smaller})} \sim \frac{\exp(M^2)}{\exp[(M-E_a)^a]}\sim\exp(2ME_a G)

\] where I restored Newton's constant in the final result. All purely numerical factors are ignored. This result is still the quasi-Boltzmannian \(\exp(C\beta E_a)\) with some unknown numerical constant \(C\). Well, the calculation was really more appropriate for a static observer but even for a freely infalling one, it should still be true that the action of a creation operator creates a larger and heavier black hole. In other words, the annihilation operators produce a lighter black hole with fewer states, and therefore the excited states are in one-to-one correspondence with the smaller number of states of a lighter black hole.

Even if the calculation above is wrong despite the tolerance for errors in the numerical factors (if the parameteric dependence is different, and I hope it is), I think it's true that a fixed-mass black hole has fewer eigenstates with \(N_a=1\) than those with \(N_a=0\), so it's more likely that we will see empty modes. This likelihood is becoming overwhelming for modes that are sufficiently localized on the event horizon (those proportional to \(Y_{LM}\) with a larger \(L\)). It means that if you pick a generic state such as the \(N_b=5\) eigenstate and decompose it to the \(N_a\) eigenstate basis, most of the terms will still correspond to \(N_a=0\) which means that there will be a near-certainty that you will measure \(N_a=0\) even though \(N_a,N_b\) refuse to commute.

The fact that \(N_a\neq 0\) may happen shouldn't be shocking. Look at a younger black hole and you will see that the interior can't be quite empty. It takes \({\mathcal O}(r_s)\) of proper time to suck "most of the material" of the star from which the black hole was created but because some of the material recoils etc., there's a nonzero amount of material inside the black hole at later times, too.

Joe neglects the fact that \(N_a=0\) is only an approximately valid statement and uses the strict \(N_a=0\) to derive a paradox. I think that \(N_a=0\) is just approximate and in fact, it's an interesting challenge to use the laws of quantum gravity – or specific laws in a formulation of string theory – to derive the percentage of states that have \(N_a=1\), for example. Classically, almost all microstates must correspond to an empty interior (as seen by an infalling observer) because the highest-entropy, dominant microstates are those that (because of the second law of thermodynamics) appear "later" once the black hole is sufficiently stabilized, almost perfectly spherical, and after it has consumed the star material and its echoes. The reason behind \(N_a\approx 0\) is therefore "entropic".

I don't know what the exact parametric dependence is so most of the formulae above were just "proofs of a concept" but I do think it shows that Polchinski et al. have overlooked a loophole that is arguably more plausible than all the loopholes they have discussed. The loophole says that the emptiness of the black hole interior simply isn't perfect but it is very good for large black holes and localized modes (certainly no deadly firewalls!). The equivalence principle at long distance scales, unitarity, and other assumptions of quantum mechanics and low-energy effective field theory may be preserved when complementarity is allowed to do its job and declare the information inside and outside the black hole as "not quite independent information".

And that's the memo.